
Pourquoi de nombreuses maladies mettent beaucoup plus de temps à se développer chez certaines personnes touchées que chez d'autres ? Il se trouve que presque dans toutes les maladies, il arrive un moment « où le « bien » est dépassé par le « mal » » et si ce modèle de prolifération est rapide pour la majorité des personnes, il peut être beaucoup plus lent pour quelques patients. Cette loi de « Sartwell » (1950) n’a jamais été totalement expliquée. Cette équipe de l'Université de Cornell (New York) s’y attache et montre, dans la revue eLife, que les niveaux de santé et d'exposition à l'agent pathogène peuvent certainement jouer un rôle, mais que finalement ils ne sont pas déterminants.
Ainsi, de nombreuses maladies -avec des exemples bien documentés pour la typhoïde, la rougeole, la poliomyélite, le paludisme et même le cancer – mettent beaucoup plus de temps à se développer chez certaines personnes touchées que chez d'autres. Et si l’on sait depuis plus de 60 ans que les périodes d'incubation de nombreuses maladies suivent un certain schéma, soit une apparition relativement rapide des symptômes dans la plupart des cas et une période d’incubation beaucoup plus longue chez d'autres personnes. Cette étude apporte à la compréhension de cette variabilité.
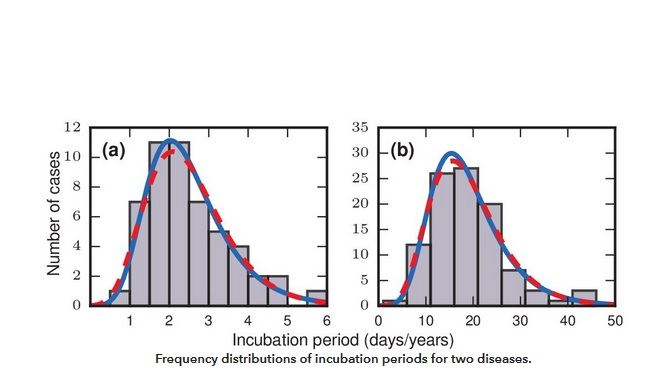
La période d'incubation de nombreuses autres maladies suit une distribution asymétrique approximativement log-normale. Ce modèle pose toujours la question ouverte de son omniprésence. Les chercheurs proposent ici une explication basée sur 2 concepts :
- le collecteur de coupons : un collectionneur cherche à avoir toutes les coupons d'une collection mais lorsqu’il les achète, il ignore le numéro du coupon. Le problème est de savoir combien il devra faire d'achats pour avoir la collection complète.
- la marche aléatoire : un promeneur effectue une succession de pas aléatoires. Ainsi, à chaque instant, le prochain pas dépend du pas précédent, mais pas des précédents. Sa trajectoire « perd la mémoire » à mesure qu'elle avance dans le temps.
Concrètement, les chercheurs font l’hypothèse que 2 sujets ayant le même état de santé sont soumis à des expositions de même niveau d'agents également pathogènes mais qu’ils peuvent, par hasard seulement, montrer des temps d’incubation extrêmement différents. Ils développent un modèle mathématique dans lequel le hasard joue un rôle clé et qui permet de calculer combien de temps il faut à un virus ou à une cellule cancéreuse pour s'emparer d'un réseau de cellules saines.
Leur modèle mathématique confirme le principe d’une distribution proche de la « lognormale », ce qui signifie que les périodes d'incubation elles-mêmes, sont normalement distribuées. Ce modèle confirme l’exemple d’un dîner en 1914 en Californie, au cours duquel 93 personnes ont été infectées par la fièvre typhoïde. Ici, sur la base de l'heure connue d'exposition et l'apparition des symptômes pour ces 93 cas, il ressort que les périodes d'incubation vont de 3 à 29 jours, avec une période d’incubation médiane de 6 jours. Cependant certains convives ont mis 4 semaines pour tomber malade. La découverte que les périodes d'incubation tendent à suivre des distributions asymétriques, avec des symptômes se développant rapidement pour la plupart des gens et des périodes d’incubation beaucoup plus longues pour d’autres, ressort également d’enquêtes épidémiologiques sur des incidents dans lesquels de nombreuses personnes ont été exposées, au même moment, à un agent pathogène.
La virulence du pathogène, un facteur majeur de distribution des temps d’incubation : le modèle montre que lorsque la virulence de l'agent pathogène est élevée, la période d’incubation suit plutôt le concept du collecteur de coupons, lorsque la virulence du pathogène est neutre ou faible, la période d’incubation suit plutôt celle de la marche aléatoire.
Aucun de ces effets n'exige d'hétérogénéité de la part de l'hôte.
Si les auteurs admettent qu’il est difficile de généraliser trop largement leur théorie, ils montrent, dans leur article, qu’elle « résiste à d'innombrables simulations et calculs analytiques » et qu’elle pourrait être utile pour expliquer non seulement la prolifération des épidémies, mais aussi d'autres exemples de phénomènes viraux, en informatique ou en finance …
Source: eLife Dec 21, 2017 DOI: 10.7554/eLife.30212.003 Evolutionary dynamics of incubation periods

Laisser un commentaire